From Bioblast
Description
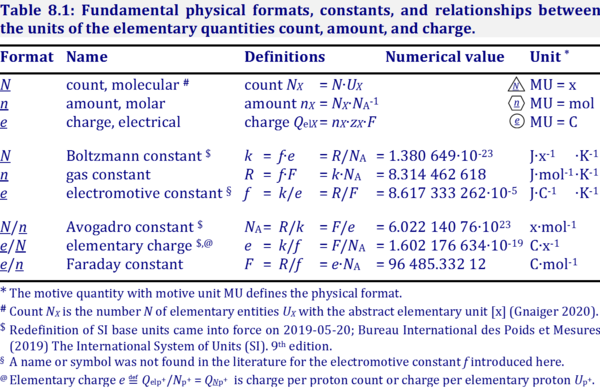
The electrochemical constant f has the SI unit for energy per charge per temperature [J·C-1·K-1].
f = k·e-1, the Boltzmann constant k divided by the elementary charge e.
f = R·F-1, the gas constant R divided by the Faraday constant F.
Abbreviation: f [J·C-1·K-1]
Reference: Gnaiger 2020 BEC MitoPathways
Communicated by Gnaiger E 2020-11-24
Canonical comments on IUPAC definitions in the context of charge
Charge of the proton versus charge per proton
- Proton charge is the elementary charge e [C·x-1], which is charge per count of protons.
Qel ≝ Qelp+ [C]
e ≝ QNp+ = Qel·Np+-1 [C∙x-1]
- The distinction of charge of particles versus charge per single particle is not made sufficiently clear by IUPAC, when defining "-e is the charge of an electron" — it must be corrected to "-e is the charge per electron".
- For comparison, the name "charge density of electrons" is used by IUPAC with symbol ρ [C·m-3]. Dividing ρ by the count concentration of electrons [x·m-3], we obtain the unit [C·x-1] for the electron charge. Therefore, electron charge (or proton charge) is clearly the charge per particle.
Ambiguity of QB
- IUPAC (Cohen 2008 IUPAC Green Book) defines the charge number as
IUPAC: zB = QB·e-1
- Therefore, QB = zB∙e. The subscript in QB indicates per elementary entity B. This is opposite to the subscript in VB as the symbol for the volume of a substance of type B (e.g. VO2 [L]). For consistency with this convention, the symbol QelB or QelX [C] is used for indicating charge of a substance of type B or X, distinguished from particle charge as the quantity of charge per elementary entity X with symbol QNX [C∙x-1]. To avoid too long and multiple subscript levels, QNX is used instead of QUX, and the ‘el’ is dropped from QelNX. The particle charge QNH+ per hydrogen ion is identical to the definition of the elementary charge e. Therefore, the charge number of the hydrogen ion is zH+ = QNH+/e = 1. In summary:
zB = QNB·e-1
QNB = QelB·NB-1 [C∙x-1]
Keywords
- » charge QelX
- » charge number zX
- » electrochemical constant f
- » elementary charge e
- » Faraday constant F
- » hydrogen ion versus proton
- » iconic symbols
- » motive entity
- » particle charge QNX
- Bioblast links: Charge - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Normalization of charge and iconic symbols
- Iconic symbols show the quantity, the format of the normalization in the subscript (N, n, e), and the entity specified in the subscript (X). The normalized quantities are per X. In the quantities QelX, NX, nX, VX, mX, the subscript X without attachment to a format indicates the quantity of X.
Quantity Unit Normalized for quantity Unit Iconic symbol Unit Practical symbol Quantity charge QelX [C] / count NX [x] = QNX [C·x-1] particle charge (IUPAC: QB) charge QelX [C] / amount nX [mol] = QnX [C·mol-1] charge number times Faraday constant charge QelX [C] / volume VX [m3] = QVX [C·m-3] ρel charge density charge QelX [C] / mass mX [kg] = QmX [C·kg-1] specific charge count NX [x] / charge QelX [C] = NeX [x·C-1] amount nX [mol] / charge QelX [C] = neX [mol·C-1] volume VX [m3] / charge QelX [C] = VeX [m3·C-1] ρel-1 mass mX [kg] / charge QelX [C] = meX [kg·C-1]
- Bioblast links: SI base units - >>>>>>> - Click on [Expand] or [Collapse] - >>>>>>>
- Entity, count, and number, and SI base quantities / SI base units
Quantity name Symbol Unit name Symbol Comment elementary UX elementary unit [x] UX, UB; [x] not in SI count NX elementary unit [x] NX, NB; [x] not in SI number N - dimensionless = NX·UX-1 amount of substance nB mole [mol] nX, nB electric current I ampere [A] A = C·s-1 time t second [s] length l meter [m] SI: metre mass m kilogram [kg] thermodynamic temperature T kelvin [K] luminous intensity IV candela [cd]
- Fundamental relationships
- » Avogadro constant NA
- » Boltzmann constant k
- » elementary charge e
- » Faraday constant F
- » gas constant R
- » electrochemical constant f
- Fundamental relationships
- SI and related concepts
References
- Gnaiger E (2020) Mitochondrial pathways and respiratory control. An introduction to OXPHOS analysis. 5th ed. Bioenerg Commun 2020.2 - »Bioblast link«
MitoPedia concepts:
Ergodynamics